UN POCO DE HISTORIA

INTRODUCCIÓN 

La arquitectura monumental de la III Dinastía y la IV Dinastía de Egipto es una prueba notable de que los egipcios de esa época tenían conocimientos relativamente sofisticados de geometría, especialmente en el estudio de los triángulos; si bien ningún documento matemático del Antiguo Imperio ha llegado hasta nosotros.

Figura del triángulo representada en el problema R51 del papiro Rhind.El cálculo del área de esta figura se analiza en los problemas R51 del papiro Rhind, M4, M7 y M17 del papiro de Moscú, que datan todos del Imperio Medio. El problema R51 constituye en la historia mundial de las matemáticas, el primer testimonio escrito que trata del cálculo del área de un triángulo.

Enunciado del problema R51 del papiro Rhind:

equivalente a la fórmula común utilizada en nuestros días: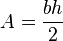

Ejemplo de cálculo de un triángulo de tierra. Si alguien te dice: un triángulo de 10 khet sobre su mryt y de 4 khet de base. ¿Cuál es su área? Calcular la mitad de 4, que es 2 para formar un rectángulo. Multiplica 10 por 2. Esta es su área.El término mryt significa probablemente la altura o el lado. Sin embargo, la fórmula utilizada para calcular el área hace pensar en la interpretación en favor de la primera solución. El escriba tomaba la mitad de la base del triángulo y calculaba el área del rectángulo formado por ese lado y la altura; es decir

equivalente a la fórmula común utilizada en nuestros días:

El hecho de que un triángulo de lados 3-4-5 es un triángulo rectángulo también era conocido por los antiguos egipcios y mesopotámicos.

Euclides, en el Libro I de sus Elementos , hacia el 300 antes de Cristo, enunció la propiedad de la suma de los ángulos del triángulo.

 Podemos concluir que así como el estudio de los números naturales surgió de problemas prácticos, el estudio de la geometría  en nuestro caso el origen de los triángulos, se desarrollo por la necesidad de medir el área de superficies de terreno (o de la tierra en general).

La historia de la Matemática nos revela que los hombres del antiguo Egipto debían restablecer los límites de sus campos después de cada crecida del río Nilo. El problema era complicado, pero la tarea se facilito considerablemente cuando se dieron cuenta de que podían dividir el terreno por medio de triángulos apropiados y así restablecer líneas imaginarias que delimitaban propiedades.